Postulates are basic assumptions or principles that are regarded as true without requiring proof. They act as the foundational elements for logical reasoning and the formulation of theories, especially in fields such as mathematics, geometry, and logic. Postulates play a crucial role in constructing systems of knowledge as they lay down the fundamental truths upon which other propositions (known as theorems) are constructed.
1) Meaning and Origin
The term “postulate” is derived from the Latin word postulatum, which translates to “that which is assumed.” In the realms of classical philosophy and mathematics, postulates were fundamental statements that were so evident and self-explanatory that they did not necessitate proof. They served as the building blocks for developing more intricate concepts through deductive reasoning.
Previous Explanation
In the context of Euclidean geometry, postulates hold particular importance. Euclid, a renowned Greek mathematician, established five essential postulates in his influential work, The Elements, around 300 BCE. These five postulates constitute the cornerstone of classical geometry. For instance, one of Euclid’s well-known postulates states: “A straight line segment can be drawn joining any two points.” This assertion is accepted as true within the Euclidean framework without requiring proof.
1) Role in Mathematics
In the field of mathematics, postulates are similar to axioms. These terms are occasionally used interchangeably, although a subtle distinction is often recognized: postulates typically denote assumptions within a particular mathematical framework (such as geometry), whereas axioms represent broader logical principles.
Mathematical frameworks depend significantly on postulates to establish their structure and functionality. For instance, in arithmetic, we accept certain postulates such as “For any number a, a + 0 = a,” which forms the foundation of the addition operation. From these postulates, more intricate properties and formulas are developed.
Logical Frameworks and Axiomatic Systems
An axiomatic system consists of a collection of axioms or postulates that establish a mathematical framework. Within these systems, theorems are formulated by utilizing rules of inference on the postulates. This deductive methodology guarantees both consistency and logical validity. Notable instances of axiomatic systems encompass Euclidean geometry, Peano arithmetic (pertaining to natural numbers), and set theory (including Zermelo-Fraenkel set theory with the Axiom of Choice—ZFC).
For a postulate to serve a purpose in a logical or mathematical framework, it should ideally possess:
- Consistent – It does not conflict with other postulates.
- Independent – It cannot be inferred from other postulates within the system.
- Simple and Clear – It is straightforward to comprehend and implement.
- Sufficient – In conjunction with other postulates, it facilitates the derivation of significant theorems.
- Scientific and Philosophical Applications
Postulates extend beyond the realm of mathematics. Within the fields of science and philosophy, they frequently act as fundamental assumptions upon which theories are constructed. For instance, in the domain of physics, Einstein’s theory of special relativity relies on two key postulates:
- The principles of physics remain consistent across all inertial frames.
- The velocity of light in a vacuum is invariant for all observers, irrespective of their motion.
These premises are not derived from other physical laws; rather, they are accepted as foundational truths from which the remainder of the theory is constructed and empirically validated.
BOOLEAN POSTULATES AND LAWS:
(a) A + B = B + A
(b) A B = B A
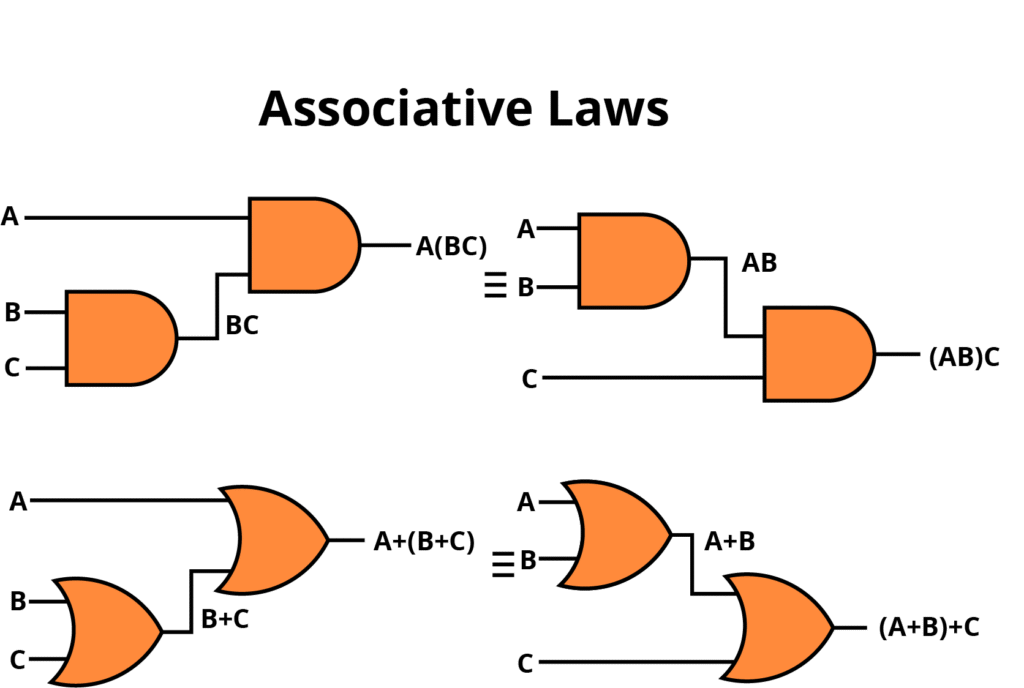
Associate Law
(a) (A + B) + C = A + (B + C)
(b) (A B) C = A (B C)
Distributive Law
(a) A (B + C) = A B + A C
(b) A + (B C) = (A + B) (A + C)
Identity Law
(a) A + A = A
(b) A A = A
(A) AB + AB = A
(B) (A+B)(A+B) = A
Redundancy Law
(a) A + A B = A
(b) A (A + B) = A
De morgan’s
(a) 0 + A = A
(b) 0 X A = 0
Abrogation law
(a) 1 + A = 1
(b) 1 X A = A
Negotiation Law
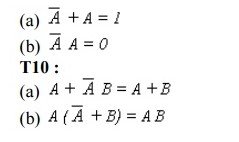
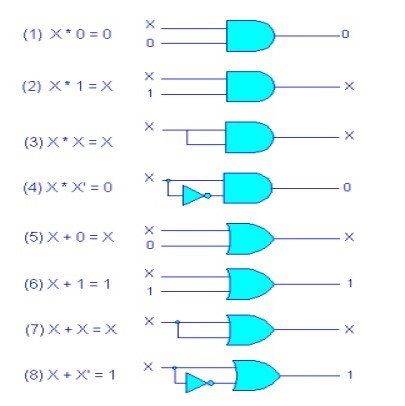
Boolean Theorems
Investigating the various Boolean theorems (rules) can help us to simplify logic expressions and logic circuits.
Boolean postulates are
— The Commutative Law of addition for two variables.
A + B = B + A
— The Commutative Law of multiplication for two variables.
A . B = B . A
— The Associative law of addition with multiplication is written as
A + (B + C) = A +B +C
— The Associative law of multiplication with addition is written as
A . (B . C) = (A . B) . C
— The Associative law of multiplication with addition is written as
A . (B + C) = A . B + A . C
— The Associative law of addition with multiplication is written as
A + (B . C) = (A + B) . (A + C)

Conclusion
Postulates serve as fundamental instruments in both logical and scientific reasoning. They establish the foundation for deductive logic, enabling the formulation of intricate systems and theorems. In fields such as geometry, algebra, or physics, postulates delineate the principles governing intellectual pursuits. Although accepted without evidence, the meticulous choice of these postulates influences the robustness, coherence, and applicability of the entire framework they support.
Grasping the concept of postulates is vital for anyone pursuing mathematics or engaging in logical analysis. They remind us that even the most sophisticated theories originate from straightforward, improvable, yet potent assumptions.
