De Morgan’s Theorems represent essential principles in Boolean algebra and digital logic. Named after the British mathematician and logician Augustus De Morgan, who proposed them in the 19th century, these theorems elucidate the behavior of logical operations such as AND and OR when negation (NOT) is applied. In the realm of digital electronics, these principles facilitate the simplification of intricate logic expressions and the design of efficient circuits utilizing universal gates (such as NAND and NOR).
The Two De Morgan’s Theorems
There exist two primary theorems, commonly known as The First and the Second De Morgan’s Law.
A⋅B=A+B
The expression NOT (A AND B) is equivalent to (NOT A) OR (NOT B)
- Second Theorem:
The negation of a disjunction (OR) is equivalent to the conjunction (AND) of the negations.
In Boolean algebra:
A+B=A⋅B
The expression NOT (A OR B) is equivalent to (NOT A) AND (NOT B)
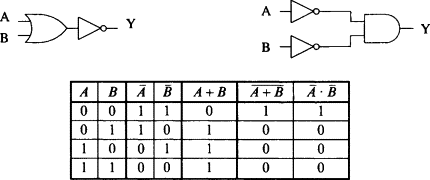
Truth Tables for Demonstrating De Morgan’s Theorems
Initial Theorem:
A | B | A·B | ¬(A·B) | ¬A | ¬B | ¬A + ¬B |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Observation:
¬(A·B) and ¬A + ¬B yield identical outputs for every possible input combination. Therefore, the theorem has been confirmed.
Second Theorem:
A | B | A+B | ¬(A+B) | ¬A | ¬B | ¬A · ¬B |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Observation:
¬(A + B) and ¬A · ¬B yield identical outcomes. The validity of the second theorem is also confirmed.
Practical Significance in Digital Logic
These theorems prove beneficial when:
- Simplifying Boolean expressions
- Transforming circuits that utilize only NAND and NOR gates
- Creating cost-effective, compact logic circuits
De Morgan’s Theorems enable the conversion of expressions containing a combination of AND/OR and NOT operators into alternative forms that may be simpler to implement or evaluate.
Instances of Utilizing De Morgan’s Theorems
Instance 1:
Simplify: 𝐴⋅𝐵⋅C
Utilize De Morgan’s First Law:
=¬A+¬B+¬C
Example 2:
Simplify: X + Y̅
Utilize De Morgan’s Second Law: =
¬X ⋅ ¬Y = X ⋅ Y
Example 3:
Given:
F = A ⋅ (B + C)
Apply De Morgan’s laws systematically:
Begin with:
𝐴⋅(𝐵+𝐶)‾=𝐴‾+(𝐵+𝐶)‾
A⋅(B+C)=A+(B+C)
Utilize De Morgan’s second law on the second term:
=𝐴‾+(𝐵‾⋅𝐶‾)=A+(B⋅C)
This formulation may be more straightforward to apply in logic gates.
Logic Gate Representation
In circuit diagrams:
- A NAND gate (NOT AND) operates as follows:
𝐴⋅𝐵‾⇒𝐴‾+𝐵‾A⋅B ⇒ A + B
A NOR gate (NOT OR) functions as:
𝐴+𝐵‾⇒𝐴‾⋅𝐵‾A+B ⇒ A ⋅ B
By applying De Morgan’s Theorems, engineers are able to transform logic circuits from one configuration to another—particularly when utilizing solely NAND or NOR gates, which are simpler to produce and more economical.
Applications of De Morgan’s Theorems
- Circuit Simplification: Aids in minimizing the quantity of gates and components.
- NAND/NOR Implementation: Transforms any logical expression into equivalent forms utilizing solely NAND or NOR gates.
- Error Detection: Engineers employ it to verify the correctness of Boolean expressions and to pinpoint redundant logic.
Programming Logic: Utilized in software engineering to streamline conditional statements.
Digital System Design: In embedded systems, De Morgan’s laws facilitate the optimization of logic flows to conserve memory and energy. Benefits in Engineering
Lowers expenses: A reduced number of gates results in less expensive hardware.
Enhances speed: More straightforward circuits operate at a quicker pace.
Boosts reliability: A smaller number of components leads to fewer potential failure points.
Conclusion
De Morgan’s Theorems serve as fundamental instruments in the realms of Boolean algebra and digital circuit design. They establish the foundation for logical transformations that enhance the efficiency and practicality of digital systems. A thorough comprehension and application of these theorems empower engineers and computer scientists to create optimized hardware and develop cleaner, more efficient logic in programming. In an era that is progressively influenced by digital systems, mastering De Morgan’s Laws is not merely advantageous—it is