In Digital Electronics, any logic circuit’s output is the function of digital inputs, and the relation between input and output can be represented using a logic table or Boolean expressions.
This Boolean expression can be represented in two forms.
- Sum of Product (SOP)
- Product of Sum (POS)
The Sum of Product Form (SOP): What is it?
The product number in the sum of the product form of representation is a logical operation of the various input variables, which may be in the complemented or true form.
A Boolean statement that involves the addition of many product terms (including AND operations) is known as the Sum of Product (SOP) form. The most often used form for digital system design and optimization. Each of the components is a combination (ANDing) of a few variables (or their negations) in SOP format; disjunction (ORing) is used to combine them all. This is highly useful, for example, for building logic circuits from truth tables or simplifying logic functions algorithmically.
Example:
A.B, A.B̅.C (example of product term)
In SOP sum refers to logical OR Operation. Therefore, in this sum of product form of expression, we perform logical or operations on different product terms. Therefore, it is known as the Sum of Product form.
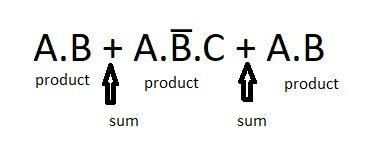
Example:
A+ B̅.C + A.C
As we can see in the above example, the
product terms(A , B̅.C , A.C) which
are created by multiplying input variables, and are then summed with each other.
SOP Form
The SOP form can be in either canonical form or non-canonical form.
1) Non-Canonical SOP Form
In this form, each product term may or may not contain all the variables of the function.
Example:
F (A, B, C) = A+ B̅.C + A.C
As we can see in the above example, the function has variables A, B, and C, but we are not including each variable in each product term. In the first product term (A), we have not included B & C. In the second product term, we (B̅.C) have not included A. While in the last product term, we have not included B.
2) Canonical SOP Form
In canonical SOP form, each product term contains all the variables of the function, where variables in each product term can be in true form or complemented form.
Example:
F (A, B) = Ā.B + A.B̅
As we can see in the above example, each product term contains all the variables that are present in the function. In the first one (Ā.B), A is present in complementary form while B is in true form. In the second one, A is present in true form while B is in complementary form.
Writing Boolean Expression for Given Truth Table in SOP Form
Suppose the following is the truth table for an electronic circuit:
A | B | C | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
The SOP form is written when the function is high. i.e, we will take conditions only in which the output is one. In the given truth table, the columns with F = 1 are the rows with high output. Now we will write a function in the form of given variables, which are A, B, and C. If we have 1 in the cell of a given variable, we will write it as it is, and if we have 0 in the given cell, then we will write its complement.
F = Ā.B.C̅ + A.B̅.C̅ + A.B̅.C + A.B.C
This is the POS in canonical form for the given truth table. Each expressions that lies between the + are known as a Midterm.
Example:
A.B.C, A.B̅.C
Therefore, we can also write it as
F (A, B, C) = M2 + M4 + M5 + M6 + M7 F(A,B,C) = ∑m(2, 4, 5, 6, 7)
We can further reduce it to non-canonical SOP form by using Boolean algebra.
F = Ā.B.C̅ + A.B̅.C̅ + A.B̅.C + A.B.C F = Ā.B.C̅ + A.B̅.[C̅ + C] + A.B.[C̅ + C] F = Ā.B.C̅ + A.B̅ + A.B F = Ā.B.C̅ + A.[B̅ + B] F = A + B.C̅
This is how we can get a non-canonical SOP form of a Boolean expression.
Creating a Truth Table with SOP Boolean Expressions
Suppose the following is the SOP expression for which we will make a truth table now
F(A, B, C) = A’B’ + AB + AC
1) As we have three input values (A, B, C), we will create 2^3 = 8 rows in the truth table to include all input combinations.
A | B | C |
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
2) For each input combination, we will put the values of the input in the expression and calculate the output:
F(A, B, C) = A’B’ + AB + AC
F(0, 0, 0) = 0’0′ + 00 + 00 = 0 + 0 + 0 = 0
F(0, 0, 1) = 0’0′ + 00 + 01 = 0 + 0 + 0 = 0
F(0, 1, 0) = 0’1′ + 01 + 00 = 0 + 0 + 0 = 0
F(0, 1, 1) = 0’1′ + 01 + 01 = 0 + 0 + 0 = 0
F(1, 0, 0) = 1’0′ + 10 + 10 = 0 + 0 + 0 = 0
F(1, 0, 1) = 1’0′ + 10 + 11 = 0 + 0 + 1 = 1
F(1, 1, 0) = 1’1′ + 11 + 10 = 0 + 1 + 0 = 1
F(1, 1, 1) = 1’1′ + 11 + 11 = 0 + 1 + 1 = 1
3) Create a truth table from the given input combinations and calculated output.
A | B | C | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
